Barycentric Coordinates

If we take a look at a Wikipedia article on barycentric coordinates we'll see that the description is very long-winded and not that easy to grasp. As a result many graphics programmer have a vague understanding of how barycentric coordinates work and why they are very useful.

What we need to understand is that the edges of a triangle on a plane form a 2D vector space. Lets call it a uv-space. We can take the edge vectors of the triangle and form a matrix that takes us from this uv-space. As you can see, a v coordinate of 1 will transform to A point, a u equal to 1 will get us to B, by adding translation we get a point in the triangle: P = (A-C)*u + (B-C)*v + C = A*u + B*v + C*(1-u-v).

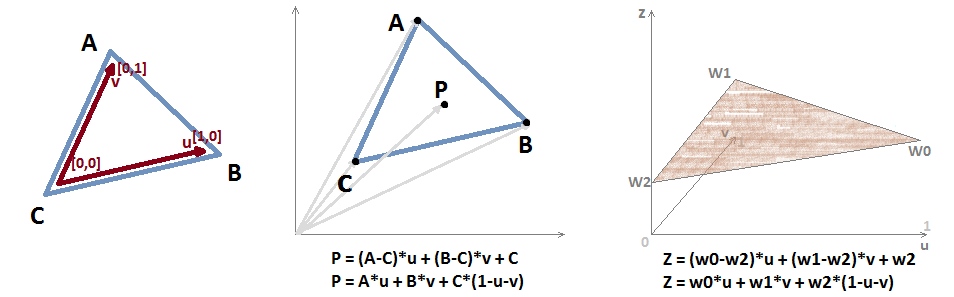
Another way of looking at it as an equation for a plane in 3D: Z = (w0-w2)*u + (w1-w2)*v + w2 = w0*u + w1*v + w2*(1-u-v), which is used for interpolating any value across the triangle. By adding the constraint u >= 0, v >= 0, u + v <= 1 we limit the domain to the triangle.

As easy it is to find the barycentrics given a triangle: we just take the inverse of the matrix and get to the uv-space as seen in the drawing. Usually in different articles the barycentric coordinates are found through normalized triangle area. But it doesn't matter because the resulting math is the same.

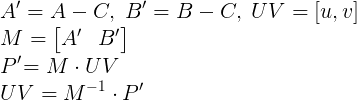
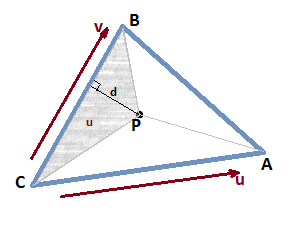
And finding the inverse of a 2x2 matrix is really easy. Now, because it just happens that barycentric coordinates are equal to normalized triangle areas (picture below), we can use that fact to find a distance to edge (trilinear coordinates): d = 2 * u * A / |B - C|, where A - the triangle area. This can be used for locating the primitive in screen space in pixel shader or for antialiasing as in DFAA.

So how do we get barycentric coordinates in a shader? There is no gl_Barycentric or similar. Actually, on GCN there is an intrinsic (there you will also find a link to a great presentation by Michal Drobot). In other cases we have the following options:

• For non-indexed geometry provide UVs with vertices. Or we can just take vertex id and index into an array {{0,0},{1,0},{0,1}} by using index % 3.

• Use a geometry shader.

• For indexed geometry things are more involved: we need to map vertices to 0,1 or 2 (to index into a shader uv-array). Sometimes it's not possible, when geometry is highly optimized and a lot of vertices are shared. But because we just need 2 bits we can pack another mapping into the same byte avoding mapping conflict. In the shader you'll have to unpack and use partial derivatives (on a flag) to decide what mapping is correct.

Also remember that we want noperspective interpolation for them. In WebGL they decided that no one needs noperspective, so there is not support for it. But we can still do non-perspective interpolation ourselves.

And to finish, here is a JavaScript demo. Drag the points to see how the barycentrics change.