A quick and easy way to print a float in base-10.

The implementation of printf for the "%f" format specifier is quite involved. I invite you to take a look: printf_fp.c. That's hard.

But there is a hack, that you could use in cases where you don't need an exact number.

The format of a 32-bit floating point in modern systems is 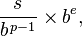where b = 2 ( ©Wikipedia ).

You could transform the base-2 exponent to base-10, take the integer part, and multiply the rest of the number with fractional part. This way you essentially get a base-10 number. I provide a draft implementation that you could use and improve.

#include <cstdio>
#include <cmath>

void print_fp( float number, int digits ) {
    union {
        float d;
        int u;
    };

    d = number;

    //deal with sign
    bool minus = u >> 31; 
    u = u & ~(1 << 31); 

    //calculate base-10 exponent
    double exp = (u >> 23) - 127;
    double exp10 = exp / log2( 10.0 );

    //adjust the number 
    u = (u & ~(0xFF << 23)) | (127 << 23);
    double d2 = double(d) * pow( 10.0, exp10 - int(exp10) ); 
    if( d2 >= 10.0 ) { d2 = d2 / 10.0; exp10+=1.0; }
    if( d2 < 1.0 ) { d2 = d2 * 10.0; exp10-=1.0; }

    static char digits[] = "0123456789";

    //print sign
    if( minus ) putc( '-', stdout );

    //print integer part
    int i = int( d2 );
    putc( digits[i], stdout );
    putc( '.', stdout );
    d2 = d2 - i;

    //print fractional part
    while( digits-- ) { 
        d2 = d2 * 10.0;
        int i = int( d2 );
        putc( digits[i], stdout );
        d2 = d2 - i;
    }

    //print exponent part
    //being a little lazy and using printf
    printf("e%d\n", int(exp10));
}


int main() {

    double d;

    //the two doubles below are special, in that a float can't distinguish between them
    //taken from Bruce Dawson post "Float Precision–From Zero to 100+ Digits"

    d = 8.589973e9;
    printf("%.10f\n", d);
    print_fp( d , 10 );

    d = 8.589974e9;
    printf("%.10f\n", d);
    print_fp( d , 10 );

}


Output:

8589973000.0000000000
8.5899735040e9

8589974000.0000000000
8.5899735040e9

Github Ideone

Be warned that I haven't done error analysis. All calculations are done in double, so I expect this to work flawlessly for floats.

I'd like to thank Bruce Dawson for his outstanding series on floating points.